Hackerearth : Counting Subarrays

Given an array A of N positive integer values. A sub-array of this array is called Odd-Even sub-array if the number of odd integers in this sub-array is equal to the number  of even integers in this sub-array.

Find the number of Odd-Even sub-arrays for the given array.

Constraints:
1 <= N <= 200,000

Problem Link – link

Solution:

On first look, this problem looks like it can be solved in O(n^3).(i.e O(n^2) for traversing all the the subarrays and O(n) for checking whether the subarray has equal number of odd and even elements.

But according to the constraint, the solution is too slow to pass.

Code

Implemented in C++

#include <bits/stdc++.h>
#define ll int64_t
using namespace std;

int main(){
	int n;
	cin>>n;
	ll a[n];
	for(int i=0;i<n;i++)
		cin>>a[i];
	
	ll cnt=0;
	
	for(int i=0;i<n;i++){
		for(int j=i+1;j<n;j++){
			int odd=0,even=0;
			for(int k=i;k<=j;k++)
				if(a[k]&1)odd++;
				else even++;
			if(odd==even)
				cnt++;
		}
	}
	
	cout<<cnt;
		
		
		
	return 0;
}

Now, let us try to find a optimal solution by making some observations. For that let us take the following example.

 

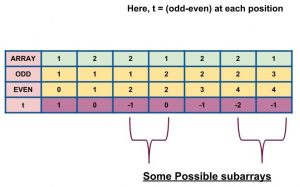
Let N be 7 and A = { 1,2,2,1,2,2,1 }. Let us find the number of odd and even integers for each position from the start. Then find t which is odd-even for each position.

From the above pic we have the following observations:

• Subarray bounded by same t value where the leftmost element is not accounted satisfies the requirement. For example, consider from 3rd column to 5th, if we exclude 2 which at 3rd position, we get {1,2} which satisfies the requirement. Similarly from 3rd column to 7th column we get {1,2,2,1} after ignoring 2.
• Thus the for each t value, we have C(n,2) ways of selecting them.
• Another important point is that we have to add an extra 0. For example, for columns 1st to 2nd, {1,2} satisfies the condition but is not counted. So adding an extra zero resolves the issue.

 

Thus, after this all is required is to count all values of t and compute their C(ti,2). So the complexity is this case would be O(MAX_N) as the max value that t can get is either N or -N.

Code

Implemented in C++

#include <bits/stdc++.h>
#define MX 1000006
#define MX1 400020
#define ll int64_t
using namespace std;

int a[MX];			// Array for storing count of each t value
			// here double sized array is used to store negative t values
int main(){
  int n;
  cin>>n;
  int o=0,e=0;
  a[MX1]++;			// Update according to point #3 of observation at 0 position, as double sized array is used
  for(int i=0;i<n;i++){
    ll b;
    cin>>b;			// element input
    if(b&1)o++;		// if odd update o which stores nos. of odd till that position
    else e++;		// else update e which stores nos. of even till that position
    int t=o-e;		// calculate t at that position
    a[MX1+t]++;		// update array accordingly
  }
  ll res=0;
  for(int i=0;i<MX;i++){	// Now, for each value int array a
    res+=((1LL*a[i]*(a[i]-1))/2);	// calculate C(n,2) i.e. no. of ways of choosing 2 things out of n
  }
  cout<<res<<"\n";		// display the result
  return 0;
}

Optional implementation hint:

Rather than using array of double size, one can use map data structure for each access. Though in that case addition and query will take O(log n) time.

Counting Sub-arrays is Published by Arnab Ghosh.
If you want to be a content writer with Gohired.in, please write at career@gohired.in or at admin@gohired.in.