Leetcode: Edit Distance

Given two words word1 and word2, find the edit distance between word1 and word2 i.e. minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

1. Insert a character
2. Delete a character
3. Replace a character

Example 1:

Input: word1 = “horse”, word2 = “ros”
Output: 3
Explanation:
horse -> rorse (replace ‘h’ with ‘r’)
rorse -> rose (remove ‘r’)
rose -> ros (remove ‘e’)

Example 2:

Input: word1 = “intention”, word2 = “execution”
Output: 5
Explanation:
intention -> inention (remove ‘t’)
inention -> enention (replace ‘i’ with ‘e’)
enention -> exention (replace ‘n’ with ‘x’)
exention -> exection (replace ‘n’ with ‘c’)
exection -> execution (insert ‘u’)

Constrains:

1 <= ( |word1| * |word2| ) <= 10^6

Question Link: Edit Distance

Solution: 

This problem looks like a typical usecase of recursion to in which we have three cases:

1. Insert a character
2. Delete a character
3. Replace a character

The way to approach these kinds of recursive problems is to assume that the all the previous characters have been fixed and the current state is what we are going to fix ( here we have to make the current state character equal). Here we can fix the current state in these three ways:

Insert a character:
When we are at a state of one less character in one word than the other, then insertion of a character can be used such as:

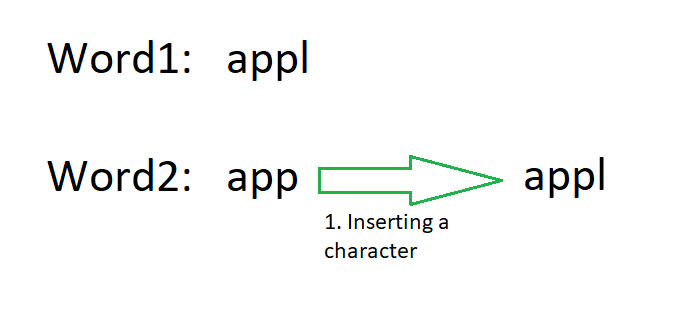
Delete a character:
When we are at a state of one less character in one word than the other, then deletion of a character can be used such as:

Replace a character:
When we are at a state of both words being same except the current state’s characters are different then replacing a character can be used such as:

But here is the main part, we don’t need to replace a character if the character at the current both states are same.

Terminating Condition:
When one of our current state reaches the end of its word, then we have to terminate by adding the inserting the remaining characters of the other word at the end of this word.

Switching Rule:
So when we are switching from one state to the next state, we need to check: If the current states have same character?

If YES, then directly go to the next state without performing any operation.

Otherwise, answer will be min (operation1, operation2, operation3) + 1.

Code:

Implemented in C++

class Solution {
public:
    // Helper fuction to calculate the answer
    int rec(string &word1, string &word2, int i, int j){

        // Base Cases where current state reaches its end
        if (i == word1.length()) return word2.length() - j;
        if (j == word2.length()) return word1.length() - i;
        
        // Checking if word is same, then directly pass
        if(word1[i] == word2[j]) return rec(word1, word2, i+1, j+1);

        // different, so taking minimum of all three
        return min( min(rec(word1, word2, i+1, j), rec(word1, word2, i, j+1)), rec(word1, word2, i+1, j+1)) + 1;
    }
    
    int minDistance(string word1, string word2) {
        //Recursive solution
        return rec(word1, word2, 0, 0);
    }
};

But the worst case complexity of this solution is 3^max(|word1|, |word2|)

Optimization:

The optimization that we require here is to use Dynamic Programming inplace of Recursion.

The difference would be how to define base cases:
Here bases cases would be when current state contains zero words of one the word. In such a case, the dp value (minimum number of oper) for that state would be length of the other word (by consecutive addition operations).

We can either use Memoization or Bottom Up approach. Here we have implemented the bottom up approach:

To understand a Bottom Up DP approach the following table can be used:

Here base conditions are used to fill first row and first column.
For the rest, we can use the Recursive Equation:

DP[i][j] :
if word1[i] == word2[j] : dp[i-1][j-1]
else : min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1

After filling the table would look like:

CODE:

Implemented in C++

class Solution {
public:
    int minDistance(string word1, string word2) {
        // DP Solution
        int n1 = word1.length(); //length of word1
        int n2 = word2.length(); //length of word2
        // declaring a dp double dimension array
        // dp[i][j] = min num of opers to perform to make
        // word1 upto length i and word2 upto length j equal
        int dp[n1+1][n2+1];

        //base conditions as discussed above
        for(int i=0;i<=n1;i++) dp[i][0] = i;
        for(int i=0;i<=n2;i++) dp[0][i] = i;
        
        // looping through all cases
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(word1[i-1]==word2[j-1]) //when current state contains same characters
                    dp[i][j] = dp[i-1][j-1];
                else //different, so minimum of all three opers with +1
                    dp[i][j] = min( min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1;
            }
        }
        
        return dp[n1][n2]; //min opers to make word1 equal to word2 or vice versa
    }
};

Here the time complexity would be O( |word1| * |word2| ) and space complexity would also be O( |word1| * |word2| ) .