LeetCode: Binary Tree Maximum Path Sum

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

Input: [1,2,3]

        1
      /    \
    2      3

Output: 6

Example 2:

Input: [-10,9,20,null,null,15,7]

         -10
         /    \
       9     20
             /    \
          15    7

Output: 42

Question Link: Binary Tree Maximum Path Sum 

Solution: 

On the first look, the problems looks like a All pairs shortest path problem. That can be solved using Floyd-Warshall algorithm which is used to find shortest distance between all the points of the graph/tree. But then complexity would be O(n^3) which is not optimal for the problem.

Further thinking reveals that we can apply Post Order Tree Traversal along with Dynamic Programming to solve this problem.

The main observation for the dp states in this problem is that there can be four ways the current node can be a part of the maximum path:

1. The Node is itself the only node in maximum path.
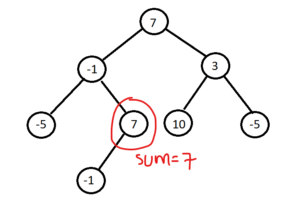
2. Node along with maximum path with the left child
3. Node along with maximum path with the right child
4. The Node along with maximum path with the left child as well as the right child

We have to check the maximum of the above four and update our answer accordingly.

So now as we know the states we have to look for the current node, what is left is to ask what we should pass above to the parent?

We obviously can’t pass the 4th one above as the cureent node is not a terminal node of the maximum path but a intermediate one. So the idea is to pass the maximum of the rest of the three above and proceed in the similar manner. After the passing each result, the tree would look something like this:

Implementation details can be understood in the code:

Code:

Implemented in C++

* Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxx; //stores the result
   //Post Order Traversal Helper Function
    int postOrder(TreeNode* root) {
        if(root==NULL) return 0; //base condition
        int left = max(0, postOrder(root ->  ;left)); //takes the maximum from left child and 0
        int right = max(0, postOrder(root - >;right)); //takes the maximum from right child and 0
        maxx = max(maxx, left + right + root->val); //calculates thg maximum possible at the current node (this comprises all four cases 1,2,3 and 4)
        return max(left, right) + root->val; //returning maximum from left, right along with current.
    }
 
    int maxPathSum(TreeNode* root) {
        maxx=root->val; //initializing with root's value
        postOrder(root); //traversing using Post Order Traversal
        return maxx; //returning maximum
    }
};