Diagonal Traversal of Binary Tree

Given a Binary Tree, print the diagonal traversal of the binary tree
Consider lines of slope -1 passing between nodes. Given a Binary Tree, print all diagonal elements in a binary tree belonging to same line.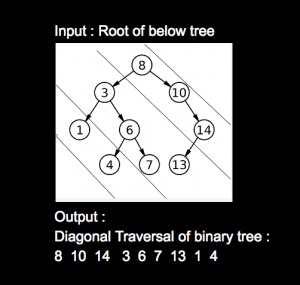
Input:
The task is to complete the method which takes 1 argument, root of Binary Tree. The struct Node has a data part which stores the data, pointer to left child and pointer to right child.
There are multiple test cases. For each test case, this method will be called individually.

Output:
The function should print out the diagonal traversal of the binary tree.

Constraints:
1 <=T<= 30
1 <= Number of nodes<= 100
1 <= Data of a node<= 1000

Example:

Input
2
2
1 2 R 1 3 L
4
10 20 L 10 30 R 20 40 L 20 60 R

Output
1 2 3
10 30 20 60 40

There are two test cases. 
First case represents a tree with 3 nodes and 2 edges where root is 1, left child of 1 is 3 and right child of 1 is 2.  
Second test case represents a tree with 4 edges and 5 nodes.

Solution : –
Method 1 : –
Explanation : – 
Hashing helps to solve diagonal traversal problem easily The .Create an empty map where each key in the map represents a diagonal in the binary tree and its value maintains all nodes present in the diagonal. Then we do a preorder traversal of the tree and update the map. For each node, we recurse for its left subtree by increasing the diagonal by 1 and recurse for right subtree with same diagonal.

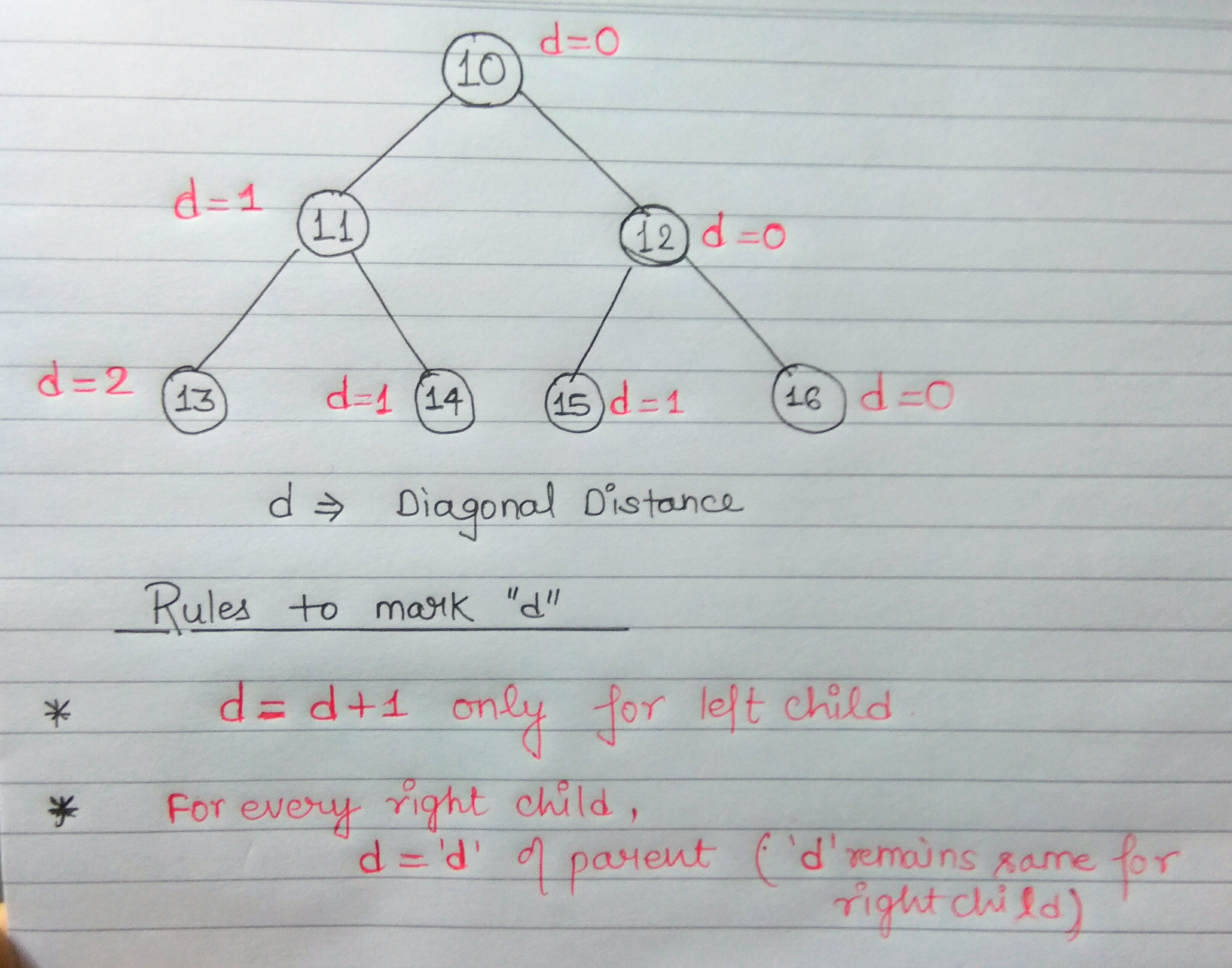
struct Node {
    int data;
    Node * left, * right;
};

void printDiagonal(Node * node, int diagonal, auto & map) {
    // base case: empty tree
    if (node == nullptr)
        return;
    // insert current node in current diagonal
    map.insert(make_pair(diagonal, node - > data));
    // recurse for left subtree by increasing diagonal by 1
    printDiagonal(node - > left, diagonal + 1, map);
    // recurse for right subtree with same diagonal
    printDiagonal(node - > right, diagonal, map);
}
void printDiagonal(Node * root) {
    // create an empty map to store diagonal element in every slope
    // we can also use map<int, vector> instead of multimap<int, int>
    multimap < int, int > map;
    // do pre-order traversal of the tree and fill the map
    printDiagonal(root, 0, map);
    // traverse the map and print diagonal elements
    int temp = 0;
    for (auto it = map.begin(); it != map.end(); it++) {
        if (temp != it - > first) {
            cout << endl;
            temp = it - > first;
        }
        cout << it - > second << ”“;
    }
}

Full code ideone link :- https://ideone.com/2gcfIL

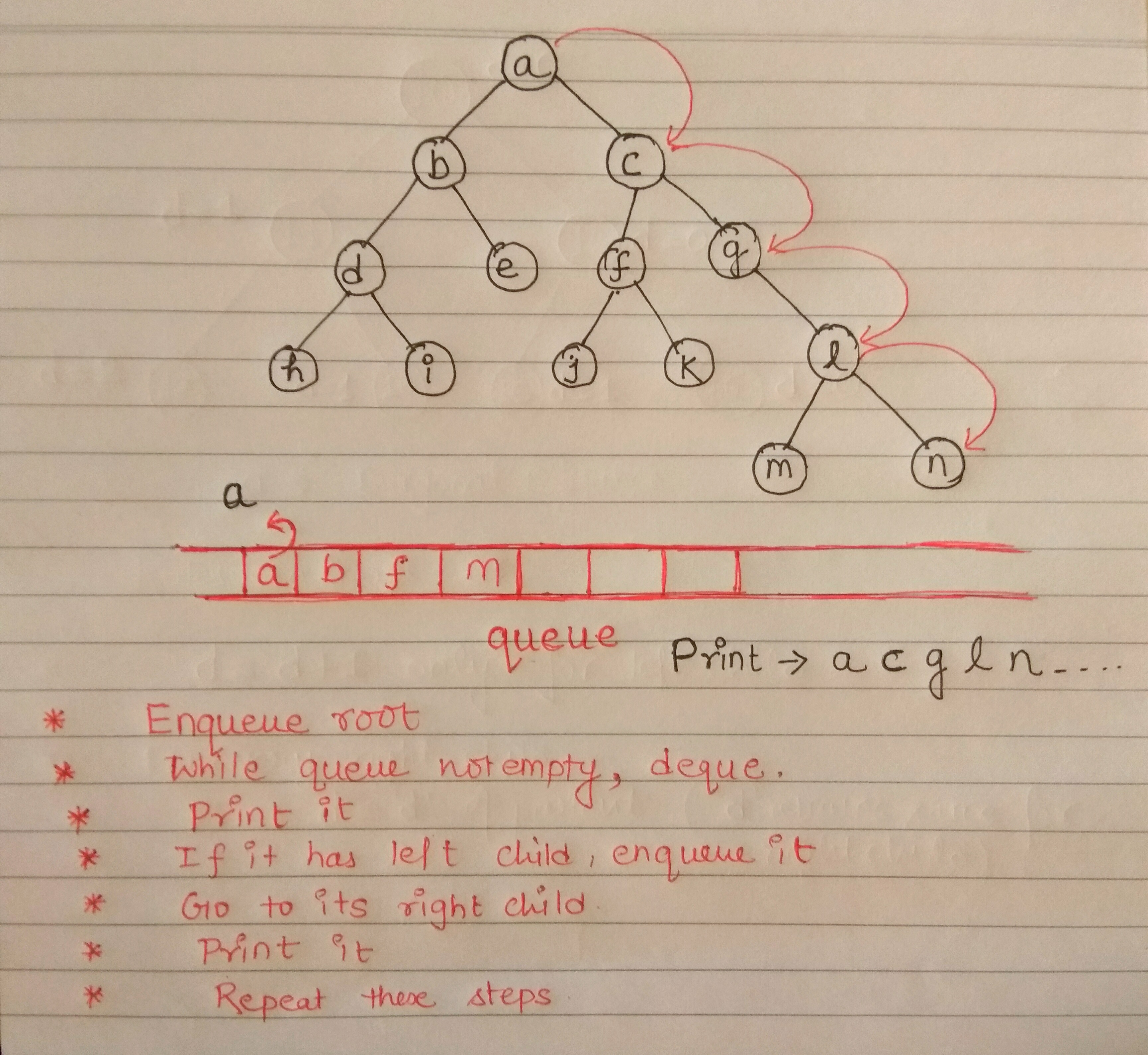
Method 2 (Using Queue) :-

Explanation : –

This method implement’s a queue to solve diagonal traversal problem . The idea is similar to level order traversal but instead of storing nodes of a level, we enqueue nodes in a diagonal.

Code(C++) : –

void diagonalPrint(Node * root) {

    queue < Node * > q;
    Node * sentinel = newNode(-1);
    while (root) {
        q.push(root);
        root = root - > right;
    }
    q.push(sentinel);
    while (q.size() != 1) {
        Node * front = q.front();
        q.pop();
        if (front != sentinel) {
            cout << front - > data << ”“;
            Node * node = front - > left;
            while (node) {
                q.push(node);
                node = node - > right;
            }
        } else {
            q.push(sentinel);
            cout << endl;
        }
    }
}

Full code ideone link :- https://ideone.com/8vvGc5