Number of Islands BFS/DFS

Problem Statement:

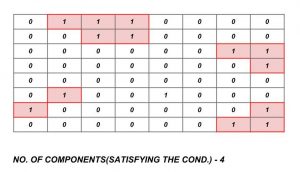
Given a 2d grid containing either values either 0 or 1 where 1 represents land and 0 represents water. You have to calculate the number of total islands in the given grid. An island is present when there are more than one 1’s in either up, down, right, left or diagonally.

NOTE- You can travel in every direction i.e at most 8 ways to travel from a cell.
 

Solution:

In these type of questions where we have to count the number components and number of elements in each element, we have to use BFS or DFS.

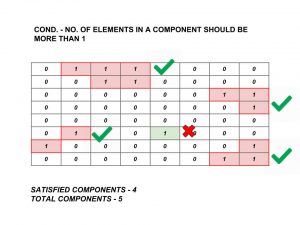
Now first we will calculate the total number of components and then check if the components contain more than one element. If the component contains more than one element then we count it or ignore it.

We will need a visited matrix to keep track of the visited places in the given grid so to avoid over-counting.

Example for counting a component or not.

Code

Implemented in C++ using BFS

#include <bits/stdc++.h>
#define mp(a,b) make_pair(a,b)
#define pp pair<int ,int >
#define ff first
#define ss second
using namespace std;

int m[102][102],vis[102][102];

int dx[]={1,1,0,-1,-1,-1, 0, 1};
int dy[]={0,1,1, 1, 0,-1,-1,-1};						// possible movement directions

int countOfIsland,r,c;

bool check(int i,int j){							// check whether a point is inside a grid or not
  return (0<=i && i<r && 0<=j && j<c);
}

void bfs(int i,int j){			    // Working of bfs:
  countOfIsland++;			        // count the start node of a component
  vis[i][j]=1;			            // make it visited
  queue<pair<int ,int > > q;		// create a queue and
  q.push(mp(i,j));			        // and add the start node to it 
  while(!q.empty()){			    // Now till the queue is not empty, do
    pp u=q.front();			        // store and pop the first entry from the queue
    q.pop();
    for(int i=0;i<8;i++){		    // Now for all its 8 neighbours,
      int x=u.ff+dx[i],y=u.ss+dy[i];	
      if(check(x,y) && !vis[x][y] && m[x][y]==1){	// check whether they are 1 and not visited
        countOfIsland++;			// if they are then increase the count,
        vis[x][y]=1;				// make them visited and
        q.push(mp(x,y));			// add them to queue
      }
    }
  }
}


int main(){  
  cin>>r>>c;
  for(int i=0;i<r;i++){
    for(int j=0;j<c;j++)
      cin>>m[i][j];
  }
  int numIsland=0;
  for(int i=0;i<r;i++){
    for(int j=0;j<c;j++){
      if(!vis[i][j] && m[i][j]==1){
        countOfIsland=0;
        bfs(i,j);
        //cout<<ct<<"\n";
        if(countOfIsland>1)numIsland++;			// count the components with no. of elements greater than 1
      }
    }    
  }

  cout<<numIsland;
  return 0;
}

Implemented in C++ using DFS

#include <bits/stdc++.h>
using namespace std;

int m[102][102],vis[102][102];

int dx[]={1,1,0,-1,-1,-1, 0, 1};
int dy[]={0,1,1, 1, 0,-1,-1,-1};			// possible direction movements

int countOfIsland,r,c;

bool check(int i,int j){			// check whether a point is inside a grid or not
  return (0<=i && i<r && 0<=j && j<c);
}

void dfs(int i,int j){				// Working of dfs :
  countOfIsland++;			       // update the count of newly discovered 1
  vis[i][j]=1;			          // make it visited
  for(int k=0;k<8;k++){			   // Now for all its neighbouring 8 cells,
    int x=i+dx[k],y=j+dy[k];							
    if(check(x,y) && !vis[x][y] && m[x][y]==1){		// check whether they are 1 and not visited till now
      //cout<<x<<" "<<y<<endl;
      dfs(x,y);			            // if thats the case then run dfs on them
    }
  }
}

int main(){  
  cin>>r>>c;
  for(int i=0;i<r;i++){
    for(int j=0;j<c;j++)
      cin>>m[i][j];
  }
  int numIsland=0;
  for(int i=0;i<r;i++){
    for(int j=0;j<c;j++){
      if(!vis[i][j] && m[i][j]==1){
        countOfIsland=0;
        //cout<<i<<" "<<j<<"\n";
        dfs(i,j);
        //cout<<ct<<"\n";
        if(countOfIsland>1)numIsland++;					// count the components with elements greater than 1
      }
    }    
  }

  cout<<numIsland;
  return 0;
}

Complexity

Both time and space complexities are O(|no. of rows|*|no. of columns|).

Number of Islands Article is Published by Arnab Ghosh.
If you want to be a content writer with Gohired.in, please write at career@gohired.in or at admin@gohired.in.