Number Theory is used a lot for solving real world problems and for the same reason It’s asked most of the time in interviews. This article marks the beginning of series of articles over Number Theory. Today we will discuss following algorithms –

• Euclid’s Algorithm For Finding GCD
• Extended Euclid’s Algorithm
• Modular Exponenetiation
• Modular Multiplicative Inverse

Euclid’s Algorithm For Finding GCD

Finding GCD( Greatest Common Divisor ) of two numbers is a very common problem which occurs as a sub problem in many large problems. The naive approach to find GCD is to iterate over all integers till the smaller of two numbers and then find the largest number which divides both numbers. The complexity of naive approach is O(min(a,b)) [a,b are numbers whose GCD is computed]. The Euclid’s algorithm reduces this complexity to O(log(max(a,b)). In this algorithm we exploit the following property –

gcd(a,b) = gcd(b,a%b)

With the above recurrence relation we can easily write recursive code to compute GCD with the base case of b = 0. In iterative implementation we will iterate until b > 0. In each iteration we will update the value of a with value of previous b and value b with modular value of previous a with previous b.

Code

The code below provides the iterative implementation of Euclid’s Algorithm of finding GCD.

int gcd(int a, int b){

    int A = max(a,b), B = min(a,b), temp;
    
    while(B > 0){
        
        temp = A % B;
        A = B;
        B = temp;

    }

    return A;

}

The complexity of computing GCD using above algorithm is O(log(max(a,b)).

Extended Euclid’s Algorithm

Extended Euclidean theorem states that, Given two numbers a and b then their GCD can be expressed as their linear combination ie.

ax + by = gcd(a,b)  x,y  Z

These coefficients x and y are used a lot while computing modular multiplicative inverse. We compute these coefficients using Extended Euclid’s algorithm. Before delving right into the algorithm let’s solve few equations first.

Let, 1. ax1 + by1 = gcd(a,b)
     2. bx2 + (a % b)y2 = gcd(b,a % b)

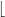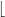
Also (a % b) = a - a/b where  represents greatest integer function.

Substituting this value in equation 2 we get,

bx2 + (a - a/b)y2 = gcd(b,a % b)

Rearranging above equation we get,

ay2 + b(x2 - a/by2) = gcd(b,a % b)

Now as discussed previously,

gcd(b,a % b) = gcd(a,b)

Finally we get,

ay2 + b(x2 - a/by2) = gcd(a,b)

Comparing the coefficients of the above equation with equation 1 we get,

x1 = y2
y1 = x2 - a/by2

The last two equations gives us the insight that the we can compute these coefficients in recursive manner. The code for recursive implementation will be almost similar to that of recursive code for simple Euclidean algorithm. All we have to do additionally is to update the values of these coefficients at the end of each recursive call according to equations derived above.

Code

Code for computing the coefficients is almost similar to code for recursive computation of GCD.

#include <bits/stdc++.h>
using namespace std;

int x,y;

void extendedEuclid(int a, int b){

	// Base case ...........
	if(b == 0){

		x = 1;
		y = 0;
		return;

	}

	extendedEuclid(b,a % b);

        // Updating coefficients with new values ................
	int temp = x;
	x = y;
	y = temp - (a/b)*y;

}

// Driver function ..........
int main(){

	int a, b;
	cin >> a >> b;

	extendedEuclid(a,b);
	cout << "x = " << x << " y = " << y << endl;

}

Complexity of computing coefficients using above algorithm is same as that of Euclidean algorithm for computing GCD ie. O(log(max(a,b))).

Modular Exponentiation

Most of the times we are required to compute a^b modulo some value m, Where b can be as large as 10¹⁸. The naive approach to solve this problem is to iterate till b and in each iteration multiply ‘a’ to result under modular arithmetic. The complexity of naive approach is O(b) and with b being as large as 10¹⁸ this approach becomes computationally infeasible.

The technique which is used to solve this problem is Binary Exponentiation. Binary Exponentiation exploits the following property –

ab = (a2)b/2 if b % 2 == 0 (ie. b is even)
ab = a * (a2)(b - 1)/2 if b % 2 == 1 (ie. b is odd)

The above two properties also serve the purpose of recurrence relation needed to write recursive code for this problem. In the recursive implementation we will check if b is odd or even. If it is even then we will solve the sub problem with new a = a * a and new b = b/2. If it is odd we will first solve the new sub problem with a = a * a and b = (b – 1)/2 and will then multiply the answer thus obtained with a. The base case will be when b = 0 in that case we will simply return value 1.

Code

The code below provides the code for both recursive and iterative implementation of above problem.

#include <bits/stdc++.h>
using namespace std;

long long int recursiveModularPow(long long int a, long long int b, long long int mod){

	// base case .........
	if(b == 0)
		return 1;

	// b is even .........
	else if(b % 2 == 0) 
		return recursiveModularPow((a * a) % mod, b/2, mod);

	// b is odd .........
	else
		return (a * recursiveModularPow((a * a) % mod, (b -1)/2 , mod)) % mod;

}

long long int iterativeModularPow(long long int a,long long int b, long long int mod){

	long long int result = 1;

	while(b > 0){

		if(b % 2 == 1){

			result *= a;
			result %= mod;

		}

		a *= a;
		a %= mod;
		b /= 2; 

	}

	return result;

}

int main(){

	long long int a, b, m;
	cin >> a >> b >> m;

	cout << iterativeModularPow(a, b, m) << endl;

}

In both recursive and iterative implementation at each iteration the value of b gets halved and the computation ends when b becomes zero. So the overall complexity of both these codes is O(log₂b).

Modular Multiplicative Inverse

Multiplicative inverse of a number x under modulo m is a number y [1, m -1] st. –

(x * y)%m = 1   ie. x-1 mod m = y

Now the multiplicative inverse of a number x under modulo m exists iff gcd(x,m) = 1. Also according to Extended Euclid’s algorithm we can represent gcd(x,m) as linear combination of x and m ie.

ax + bm = 1     a, b  Z

Taking modulo with m on both sides of above equation we get,

(ax)%m + (bm)%m = 1%m

Now as bm is multiple of hence (bm)%m = 0. Also 1%m = 1. So the above equation reduces to –

(ax)%m = 1

From the above equation we can see that the coefficient ‘a’ is the required multiplicative inverse. This coefficient can be easily computed using Extended Euclid’s algorithm that was discusses above. An another technique exists when the value under which we want to find inverse is prime but it fails for other cases. We will discuss that technique in next article till then stay tuned.

This Article is Published by Abhey Rana.
If you want to be content writer with Gohired.in Please write at career@gohired.in or admin@gohired.in