Coin Collection Dynamic Programming

Problem Statement:Coin Collection Dynamic Programming

Given a rectangular grid where each cell contains some coins. You are at the first row and you want to go to the last row with the objective of collecting the maximum number of coins on the way.

The allowed moves are down, left diagonal down and right diagonal down. And you are not allowed to step out of rectangle. So what is maximum number or coins that you can accumulate?
NOTE- You can start from any point on first row and end on any point on last row. Each entry in grid is positive i.e. greater than 0.

Solution:

Since we can start from any point on first row and end on any point on last row and collect as many coins as possible, we may get the feeling that we have to apply either greedy or dynamic programming strategy i.e. either see local maximum or global maximum. Here we can apply complete search but it would be too exhaustive as there would be a large number of overlapping subproblems.

In greedy, our strategy would be start from the point on first row with the maximum coins and then go to point on the next row out of the three points(i.e. Down or left diagonal down or right diagonal down). Thus continue this till we reach we reach the last row.

But there is a problem in using this strategy as we will see in this example.

 

Now lets see the implementation using Dynamic programming. Before that let us figure out the sub problem in this case.

Sub problem

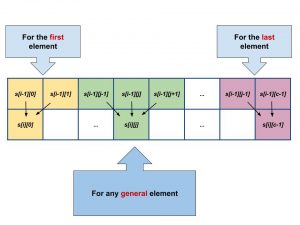
Suppose we are given a matrix S with r rows and c columns and each entry is some positive integer. Let Si,j be element in ith row and jth column.

So let’s proceed in the following manner-

• If Si,j is the first element in the ith row, then either it could have come from Si-1,j or Si-1,j+1 .
• If Si,j is the last element in the ith row, then either it could have come from Si-1,j or Si-1,j-1 .
• Else Si,j could have come from either Si-1,j or Si-1,j+1 or Si-1,j+1.

Dynamic Programming

Let us create a 2d matrix dp of dimension r*c i.e. r rows and c columns.

First we will  initialize the first row of dp with the first row of S i.e. dp[0][i]=S[0] [i] ∀ 0≤i≤c-1. Then for the rest of the rows we will solve according to the sub problem.

Thus, we will do these-

• dp[i][j]=max(dp[i-1][j] , dp[i-1][j+1])+S[i][j] for first element in ith row.
• dp[i][j]=max(dp[i-1][j] , dp[i-1][j-1])+S[i][j] for last element in ith row.
• dp[i][j]=max(dp[i-1][j] , dp[i-1][j-1] , dp[i-1][j+1])+S[i][j] for the rest of the elements.

After that we will find the maximum entry from the last row of dp, that is our answer.

Let’s see an example.

Code

Implemented in C++

#include <bits/stdc++.h>
using namespace std;
 
int s[102][102],dp[102][102];		// 2d matrix for s and dp
 
int main(){
 
  int h,w;				// h is no. of rows and w is no. of columns
  cin>>h>>w;
  for(int i=0;i<h;i++){
    for(int j=0;j<w;j++){ cin>>s[i][j];
    }
  }
  for(int i=0;i<w;i++)
    dp[0][i]=s[0][i];			// initialising first row
  for(int i=1;i<h;i++){
    for(int j=0;j<w;j++){
      if(j==0){
        dp[i][j]=max(dp[i-1][j],dp[i-1][j+1])+s[i][j];	// case where element is first in row
      }
      else if(j==w-1){
        dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+s[i][j];	// case where element is last in row
      }
      else{
        dp[i][j]=max(dp[i-1][j],max(dp[i-1][j-1],dp[i-1][j+1]))+s[i][j];	// all the rest elements
      }
    }
  }
  /*for(int i=0;i<h;i++){
    for(int j=0;j<w;j++){
      cout<<dp[i][j]<<" ";
    }
    cout<<"\n";
  }*/
  int maxx=-1;
  for(int i=0;i<w;i++){
    if(maxx<dp[h-1][i])				// finding maximum among last row of dp
      maxx=dp[h-1][i];
  }
  cout<<maxx<<"\n";
 
  return 0;
}

Complexity

Both time and space complexities are O(|no. of rows|*|no. of columns|).

 

Coin Collection Dynamic Programming Article is Published by Arnab Ghosh.
If you want to be a content writer with Gohired.in, please write at career@gohired.in or at admin@gohired.in.