Closed Parentheses checker

‏Problem Statement:

You are given 3 types of parentheses (),{},[]. Now you are supposed to check whether a given string containing some parentheses is closed or not.

Now there is a twist. Instead of checking whether a complete sequence is closed or not, you will be given a incomplete sequence containing a ‘X’ indicating a empty space and then you will have to output whether a closed sequence is possible or not.

NOTE – There will at most 5 ‘X’ in a sequence and sequence can be of at most 10000.

Required Knowledge:

Backtracking

Time Complexity:

O(n*6^{(# of ‘X’)})

 

Solution:

Here the important thing to note is that running time depends on no. of X which as defined in the question is at most 5. So we can use backtracking to solve this problem.

Now, let us see how we will apply backtracking in solving this parenthesis problem. First we will define the the base and recursion for backtracking.

The base condition is if it the sequence contains no ‘X’ then we will check whether the sequence is closed or not using the check function whose functioning we will discuss later.

The recursive condition is that we will replace each ‘X’ with one of the six parenthesis and then continue with the recursion.

Now let us discuss the functioning of the check functioning. In the check function, if the parenthesis is a left one, then we push a unique number corresponding to 3 pair of parentheses in a stack. If it is a right one, then we check whether the stack is empty or not. If it is empty then it is sure shot that it is impossible to form a closed sequence. Now if it is not, then there still remains a possibility. Now we check whether its corresponding left exists as top or not. If it exists then we continue or we return false.

 

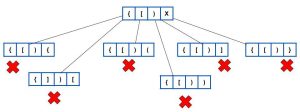
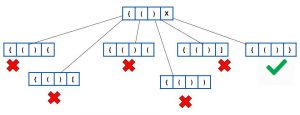
Now,let us see working for an example.

(i) For the first one

(ii) For the second case

(iii) For the third case

After this we stop, since we have already confirmed there is a closed sequence possible from the given incomplete sequence.

Code

Implemented in C++

#include <bits/stdc++.h>
using namespace std;

bool check(string s){                       // This function is used to check a parenthesis sequence 
  stack<int > st;                           // is closed or not
                                            // The idea behind this function is:
  for(int i=0;i<s.length();i++){            // 1. if it's left parenthesis, then push it
    if(s[i]=='{')				// 2. it it's right parenthesis, then check if its 
      st.push(1);				//    corresponding left occurs or not. if not then return
    else if(s[i]=='[')			//    false or else continue
      st.push(2);
    else if(s[i]=='(')
      st.push(3);
    else if(s[i]==')'){
      if(st.empty())
        return false;
      int t=st.top();
      //cout<<t<<endl;
      if(t==3){
        st.pop();
        if(st.empty())st.push(0);
      }
      else
        return false;
    }
    else if(s[i]==']'){
      if(st.empty())
        return false;
      int t=st.top();
      //cout<<t<<endl;
      if(t==2){
        st.pop();
        if(st.empty())st.push(0);
      }
      else
        return false;
    }
    else{
      if(st.empty())
        return false;
      int t=st.top();
      //cout<<t<<endl;
      if(t==1){
        st.pop();
        if(st.empty())st.push(0);
      }
      else
        return false;
    }
  }

  while(!st.empty()){
    int t=st.top();
    if(t!=0)
      return false;
    st.pop();
  }
  return true;
}

bool ans=false;				// This is a global var which contains true/false
char possible[]={'{','[','(',')',']','}'};		// This contains all possible parentheses

void rec(string s,int k,int x){			// This recursion is defined as following:
	if(ans)return;
	if(x==0){				// 1. Base case: if x=0 then check for closed
		if(ans==true)return;							
		ans=check(s);
		return;
	}
	for(int i=k;i<s.length();i++){		// 2. Recursion: change a 'X' to a parenthesis
		if(s[i]=='X'){			//    then check for the rest
			for(int j=0;j<6;j++){ 
                                s[i]=possible[j]; 
                                rec(s,i+1,x-1); 
                        } 
                } 
        } 
} 

int main(){ 
  string s; 
  cin>>s;
  int x=0;
  for(int i=0;i<s.length();i++)if(s[i]=='X')x++;
  rec(s,0,x);
  (ans==1)?cout<<"Possible\n":cout<<"Impossible\n";
  return 0;
}

 

This Article is Published by Arnab Ghosh.
If you want to be a content writer with Gohired.in, please write at career@gohired.in or at admin@gohired.in.